




桌面上放著一顆骰子,
目前1點朝上,2點朝東,3點朝南,如下圖所示:
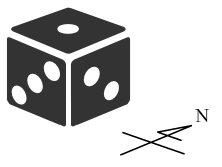
已知骰子相對的兩面點數和為7,並且能夠往東西南北四個方向翻滾。
請問要達成以下目標,各最少需要翻幾次呢?
◎本題引用自遊戲學校,網友larry提供


1.假想骰子現在正擺在棋盤格的白格子上,
翻奇數次一定會停在黑格子,偶數次則停在白格子。

翻1,3,5次會沒辦法回到原位(白格子)。
翻2次一定走原路回來,樣子不會改變。
翻4次要不走原路回來,就得繞2*2的方格,但外觀不符。
翻6次確定可行(如解答),因此6次是最少次數。
2.假想骰子現在正擺在棋盤格的白格子上,
並且把1,2,3點改為白色,4,5,6點改為黑色,
(此時相對的兩面為一黑一白)。
現在來計算看的到的面(向上、向東、向南)
以及目前的位置有幾格是黑色的:一共0格。

接著來看翻滾後會對這數量有什麼影響:
位置的黑白互換(±1),還有其中一組相對的面,
一個出現一個隱入(±1,因為是一黑一白),
數量仍維持偶數個,正是這骰子的不變量。
EX:往西再往北翻,數量依序是0+0=0,1+1=2,2+0=2



現在計算一下目標狀態的這四個位置中有幾格黑色:
總共1格(4點那面),也就是只靠翻滾是無法達成的。


